VolgaCTF 2021 Writeup

March 29, 2021

I participated in VolgaCTF 2021 as a member of WreckTheLine. The results was 14th/231 (within teams with positive points). I solved 2 crypto problems, “QR Codebook” and “Carry”. This is a writeup for those.

Crypto

QR Codebook

We were given 3 images.

img: QR which says “Helpful_Information”
img_enc: Processed QR from above img
img_flag_enc: Processed QR from FLAG QR

We didn’t have any other information, so let’s observe. My observation revealed the following:

To see images in a row, continuous numbers occur
- ex. the first raw of img_enc is [164, 164, …, 164, 164, 201, 201, …, 201, 201, 164, …, 164, 201, …, 201, …]
To see images in a column, the same patterns appear many times (16 cycles)
- ex. the first column of img_enc is [164, 25, 22, 17, 172, 23, 87, 71, 132, 139, 59, 221, 39, 32, 173, 89, 164, 25, 22, 17, 172, 23, 87, 71, 132, 139, 59, 221, 39, 32, 173, 89, …]
Column patterns are the same between img_enc and img_flag_enc
At each dot the RGB values are the same in img_enc

I guessed that there is one-to-one mapping from img[i: i+16, j] to img_enc[i: i+16, j, k] for all $i (i \equiv 0 \mod 16), j, k$ . Let’s try to find that mapping and apply it to img_flag_enc.

solve.py

import matplotlib.pyplot as plt
import numpy as np
from PIL import Image

# 0 is black, 1 (255) is white.
img_enc = np.array(Image.open("./qr.encrypted.png"))
img_flag_enc = np.array(Image.open("./flag.encrypted.png"))
img = np.array(Image.open("./qr.png"))
img_size = img.shape[0]
assert img_size == img_enc.shape[0] == img_enc.shape[1]

enc_to_dec = {}
for i in range(0, img_size, 16):
    for j in range(img_size):
        tmp = tuple(img_enc[i : i + 16, j, 0])
        if tmp not in enc_to_dec:
            enc_to_dec[tmp] = img[i : i + 16, j]

c = 0
img_flag = np.ones(img_flag_enc.shape[:2])

for i in range(0, img_flag_enc.shape[0], 16):
    for j in range(img_flag_enc.shape[1]):
        tmp = tuple(img_flag_enc[i : i + 16, j, 0])
        if tmp in enc_to_dec:
            img_flag[i : i + 16, j] = enc_to_dec[tmp]

plt.imshow(img_flag, cmap="gray")
plt.savefig("./flag.png")

There seem some incorrect dots in QR… Since each dots in QR code are bigger than 16 pixels, we can reconstruct from this image to the correct QR code in theory. But my smart phone can read this broken QR code correctly (smart!).

VolgaCTF{S0m3tim35_3C8_c4n_b3_t00_pr3dict4b13}

Carry

We were given a shift register (FCSR) and an image xor-ed by bits generated from that register. The state of the register wasn’t disclosed. The implementation of FCSR was as follow:

fcsr.py

class FCSR():
    def __init__(self, q: int, m: int, a: int):
        self.m = m
        self.q = q + 1
        self.k = int(math.log(q, 2))
        self.a = a

    @staticmethod
    def get_i(n: int, i: int) -> int:
        # right to left
        return (n & (0b1 << i)) >> i

    def clock(self) -> int:
        s = self.m
        for i in range(1, self.k + 1):
            s += self.get_i(self.q, i) * self.get_i(self.a, self.k - i)
        a_k = s % 2
        a_0 = self.a & 0b1
        self.m = s // 2
        self.a = (self.a >> 1) | (a_k << (self.k - 1))

        return a_0

    def encrypt(self, data: bytes) -> bytes:
        encrypted = b''
        for byte in data:
            key_byte = 0
            for _ in range(8):
                bit = self.clock()
                key_byte = (key_byte << 1) | bit
            encrypted += int.to_bytes(key_byte ^ byte, 1, 'big')

        return encrypted

Since the first 16 bytes of a PNG file are fixed, the 128 generated bits can be calculated.

[0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1]

From some experiments, I found that FCSR generated cyclic bits at short period when chosen parameters were bad. Looking at this problem carefully, I noticed that there was a cycle like [0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1].

solve.py

from Crypto.Util.number import bytes_to_long, long_to_bytes

from fcsr import FCSR

with open("./encrypted_png", "rb") as f:
    buf = f.read()


def xor(a, b):
    return bytes([_a ^ _b for _a, _b in zip(a, b)])


png_header = b"\x89\x50\x4e\x47\x0d\x0a\x1a\x0a" + b"\x00\x00\x00\x0d\x49\x48\x44\x52"
first_bytes = xor(png_header, buf)
first_bytes_long = bytes_to_long(first_bytes)
first_bits = list(map(int, f"{first_bytes_long:0128b}"))  # known bits: 16 * 8 = 128

cycle = [0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1]

bits = first_bits + ((8 * len(buf) - len(first_bits)) // len(cycle) + 1) * cycle
all_bytes = b""
for i in range(0, len(bits), 8):
    all_bytes += long_to_bytes(sum([b * 2 ** (7 - j) for j, b in enumerate(bits[i: i+8])]))
ans = xor(all_bytes, buf)
with open("dec.png", "wb") as f:
    f.write(ans)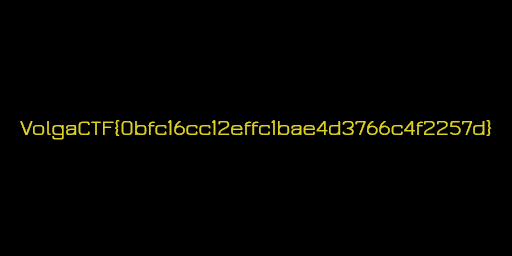

VolgaCTF{0bfc16cc12effc1bae4d3766c4f2257d}

Crypto QR Codebook Carry